1 Reeds-Shepp曲线
1.1 什么是Reeds-Shepp曲线?
想象你下班开车回家,到家后要把车停到车位里。假设你是一个喜欢追求挑战的老司机,想找一条最短的路径把车停进去。那么这样的路径是什么呢?答案就是Reeds-Shepp曲线。Reeds-Shepp曲线由Reeds和Shepp二人在1990年的论文《Optimal paths for a car that goes both forwards and backwards》[1]中提出。
1.2 Reeds-Shepp曲线是什么样的曲线?
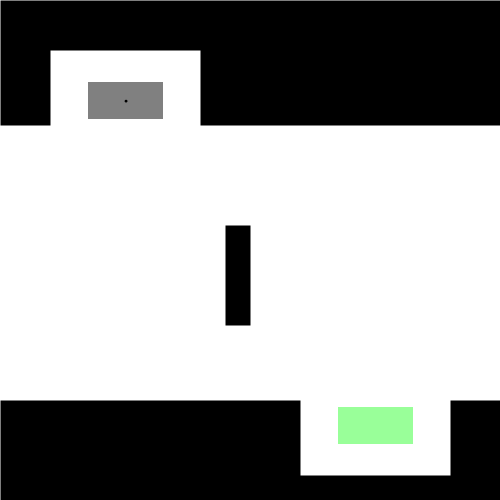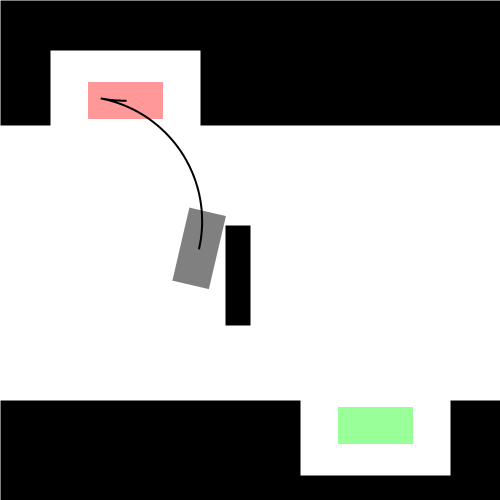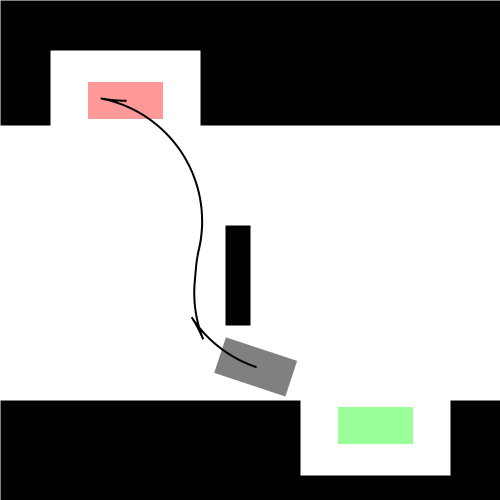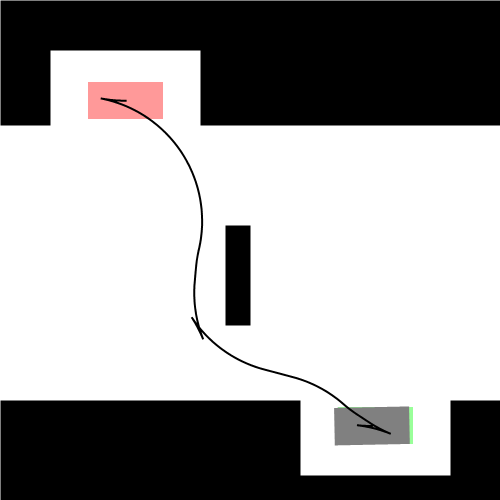
既然找的是最短路径,我们首先想到的就是直线段,那么它是直线吗?嗯…,在某些特殊情况下,它确实是直线。比如下图左所示的情况,汽车车头或者车尾刚好对准了停车位(绿色表示停车位,红色表示汽车的起始状态,灰色表示汽车)。可是实际显然不会这么简单,我们会遇到各种可能,比如下图右所示的情况:一开始车在停车位的右侧,且车头和停车位平行(例如侧位停车)。由于汽车都有一个最小转向半径,所以你不能让汽车像螃蟹一样横着开进去,这时求最短路径可就没那么容易了。图中汽车运动形成的黑色曲线就是Reeds-Shepp曲线。Reeds-Shepp曲线由几段半径固定的圆弧和一段直线段拼接组成,而且圆弧的半径就是汽车的最小转向半径。这里的路径长度是指汽车中心运动轨迹的长度,也就是所有圆弧的弧长和直线段的长度之和。
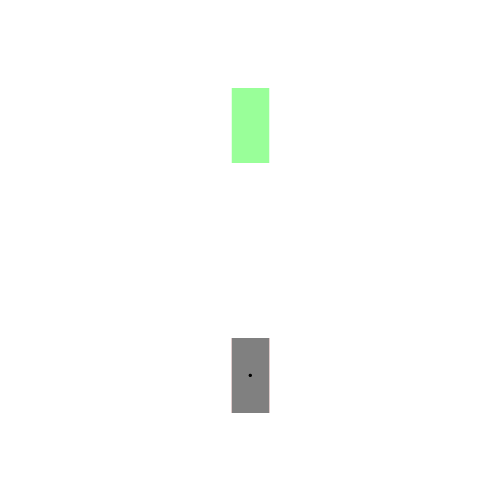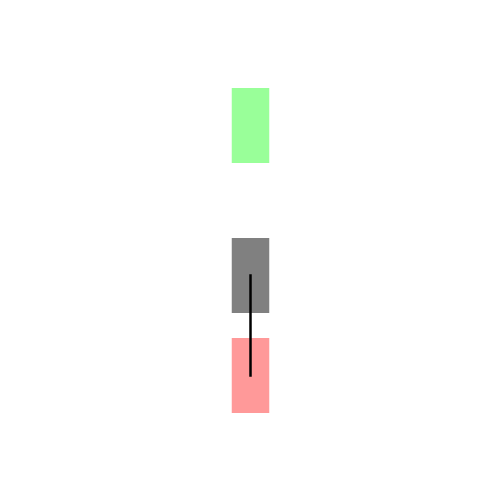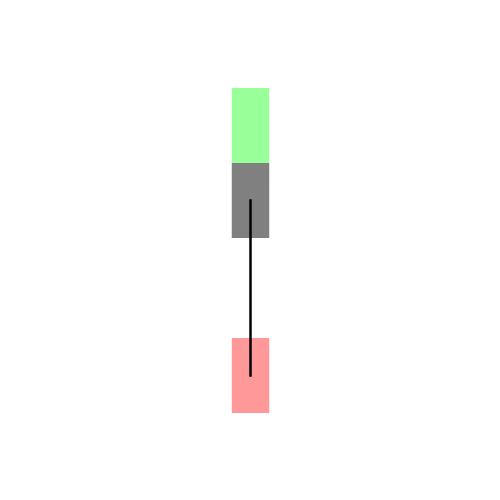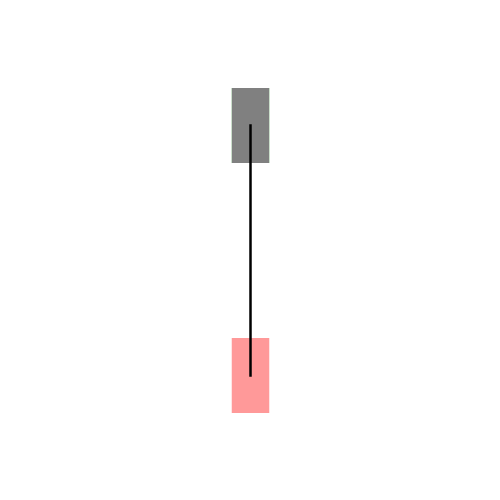
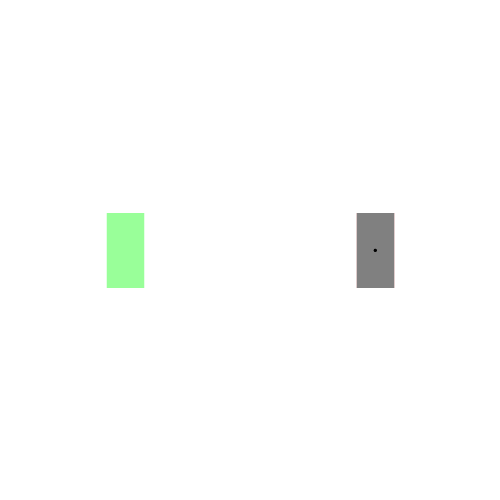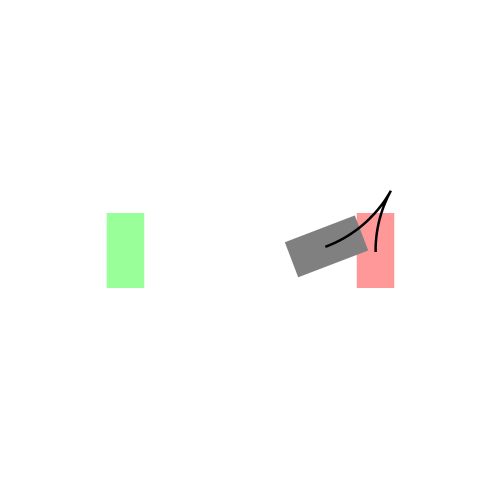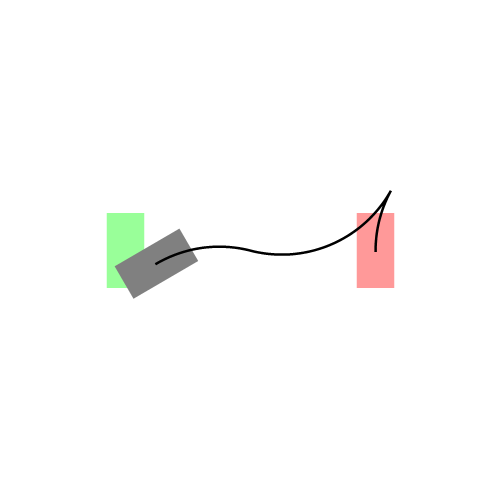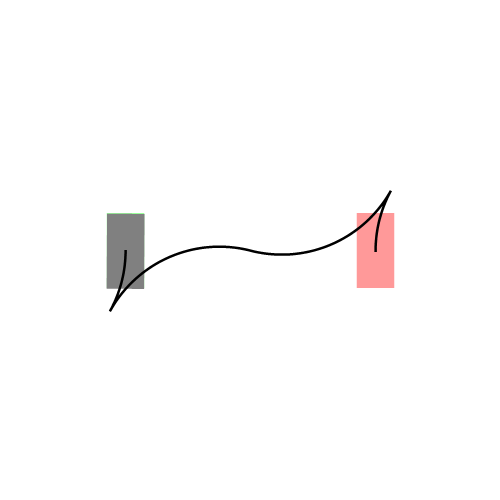
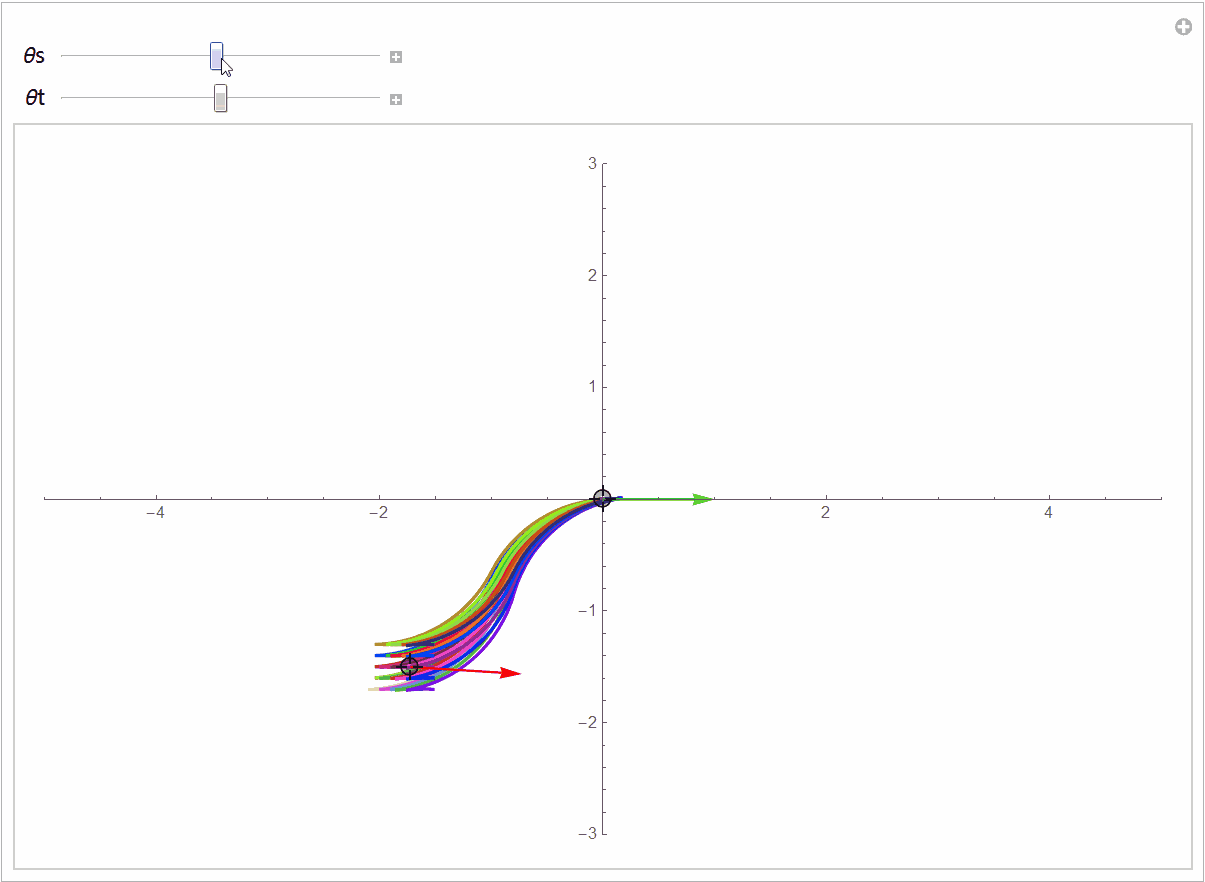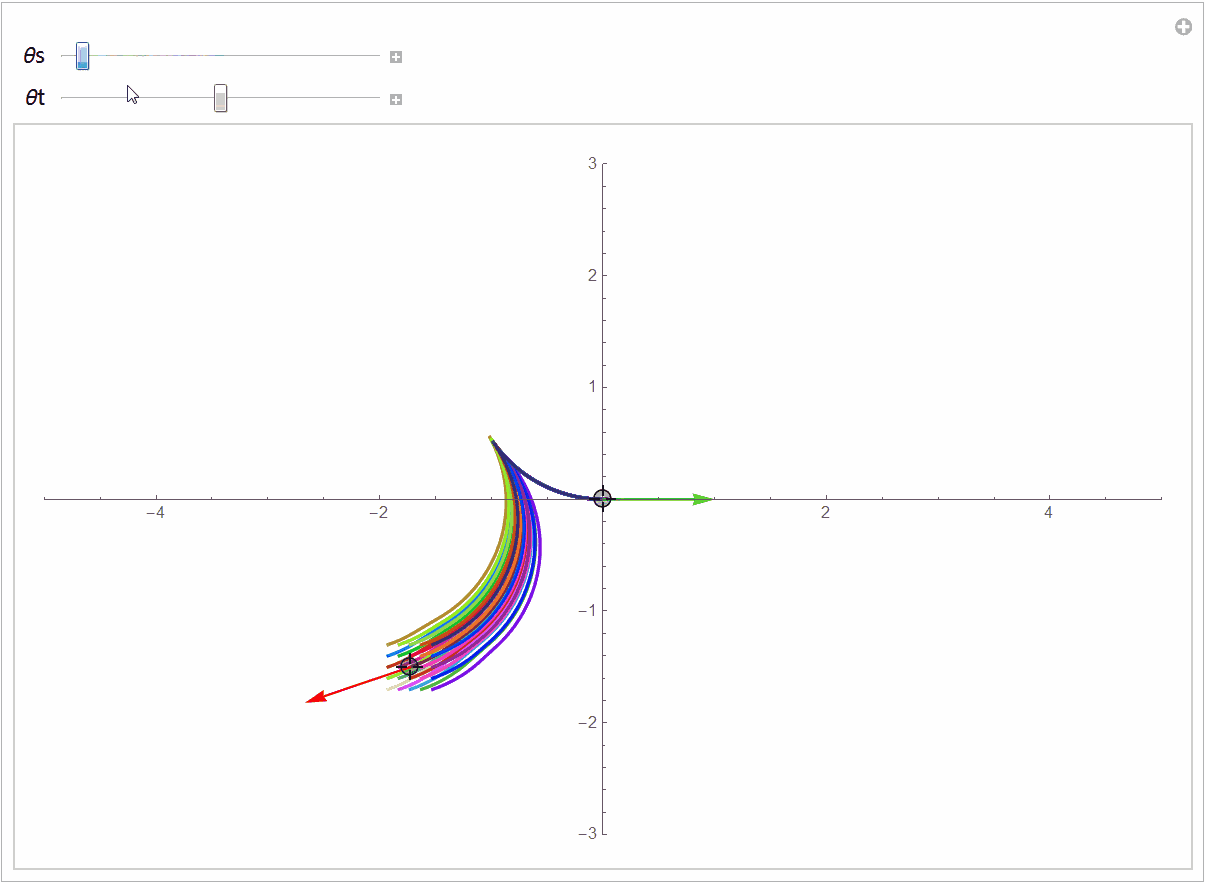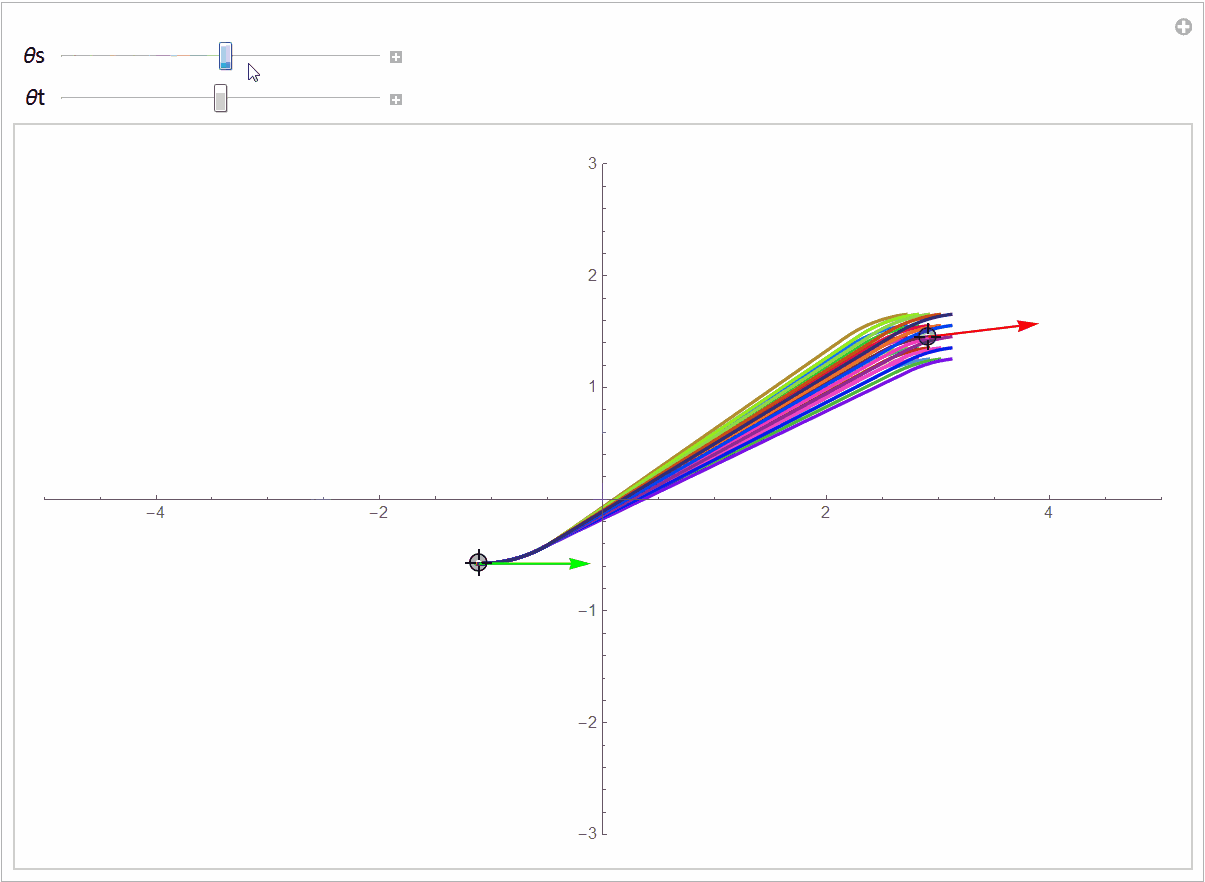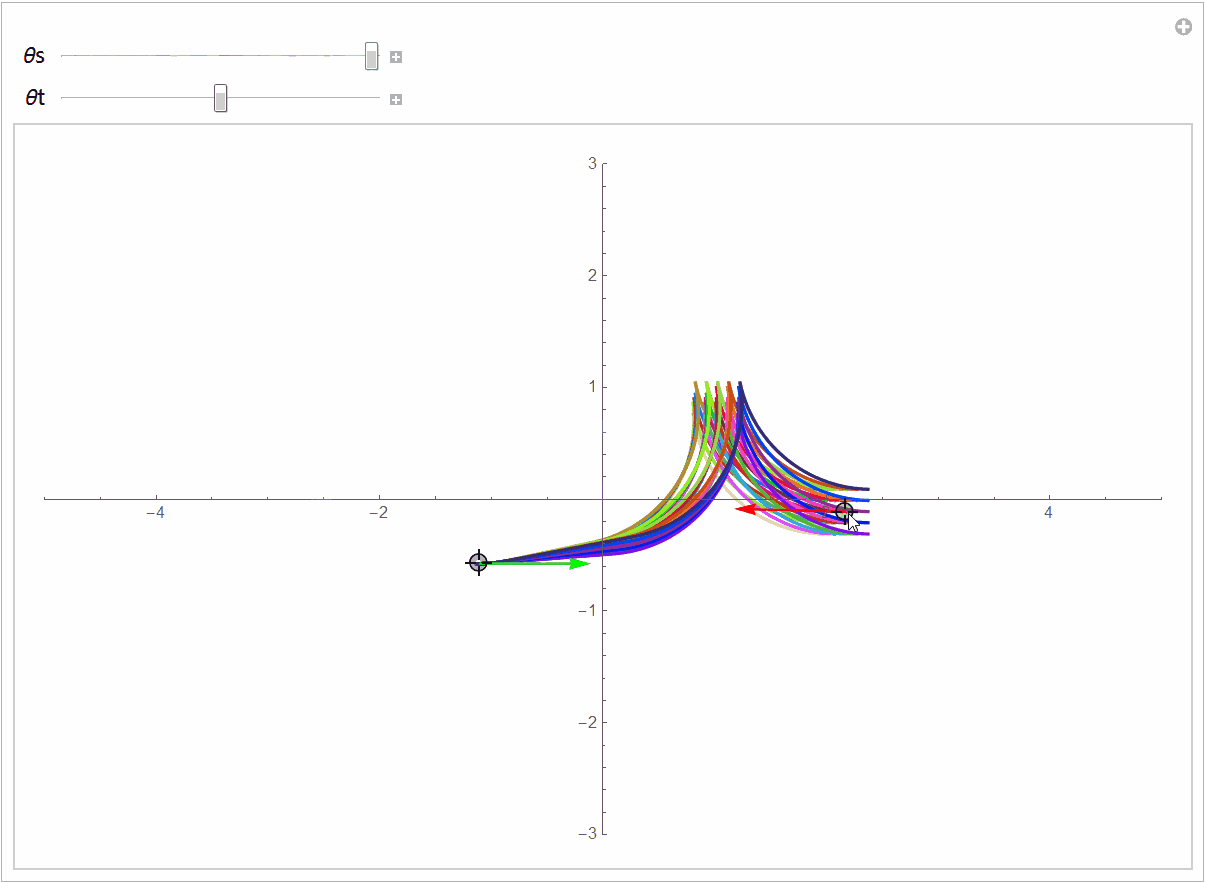
下图展示了更一般的情况,汽车从不同的初始位置和朝向进入同一个停车位:
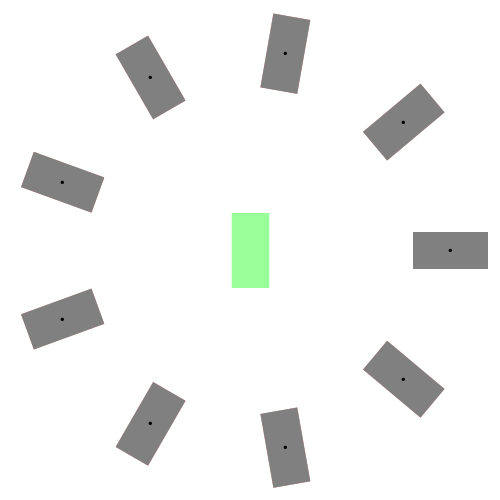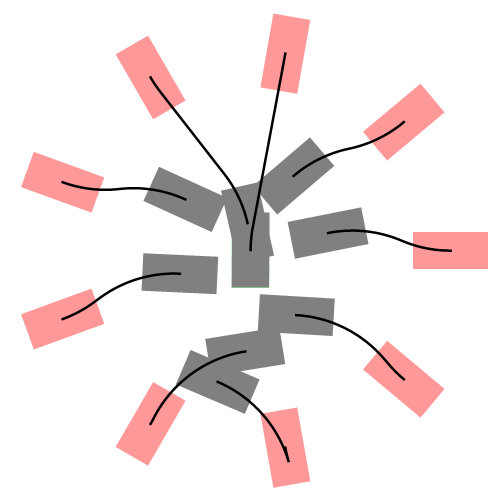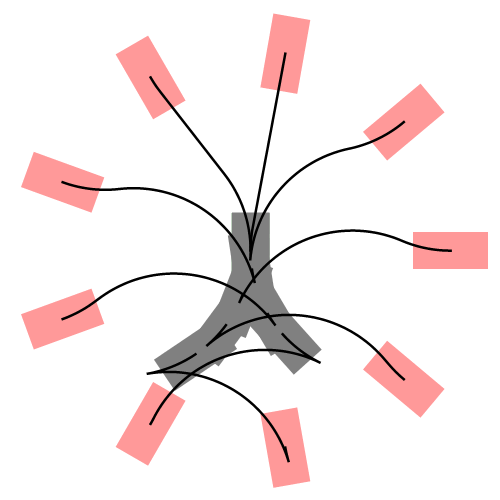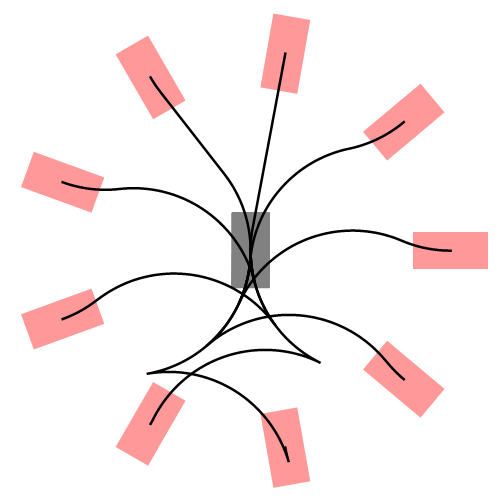
1.3 Reeds-Shepp全部曲线
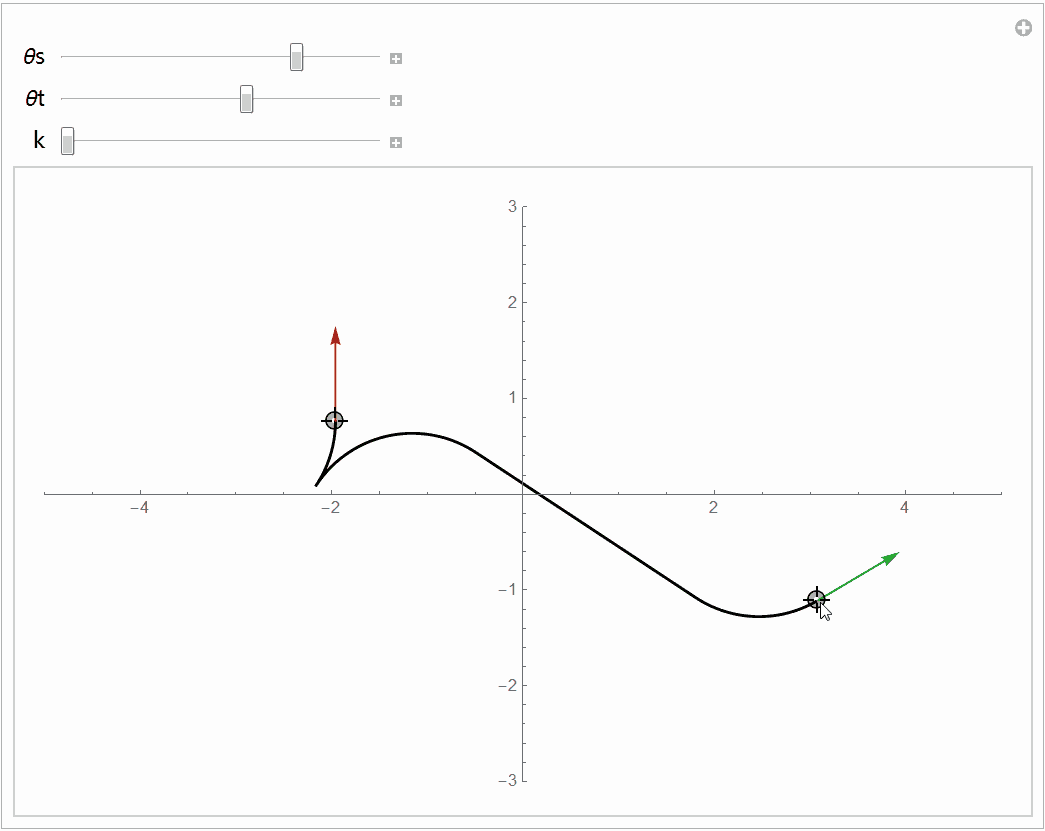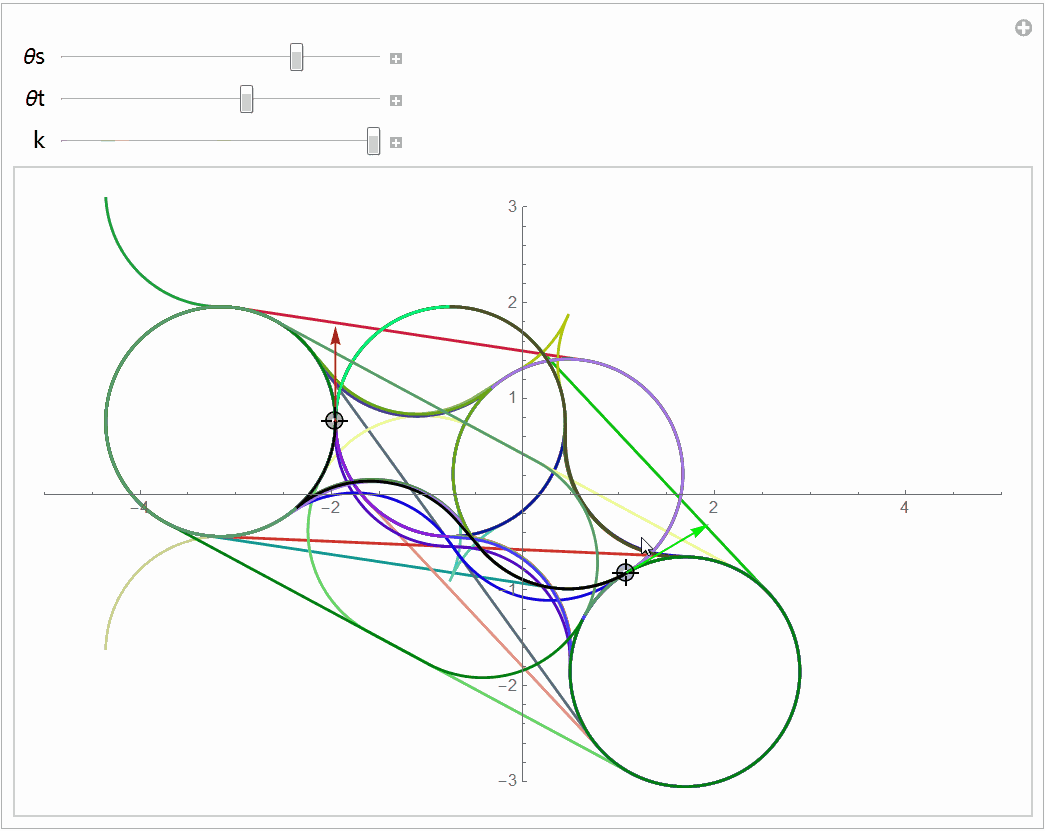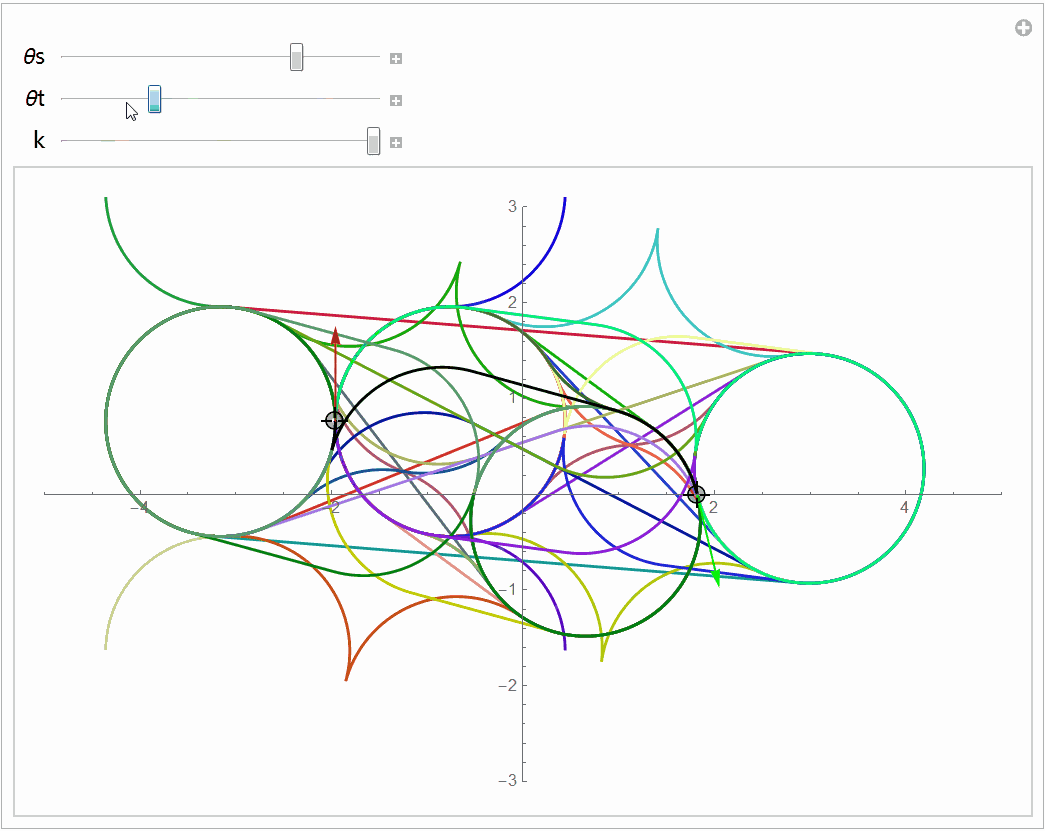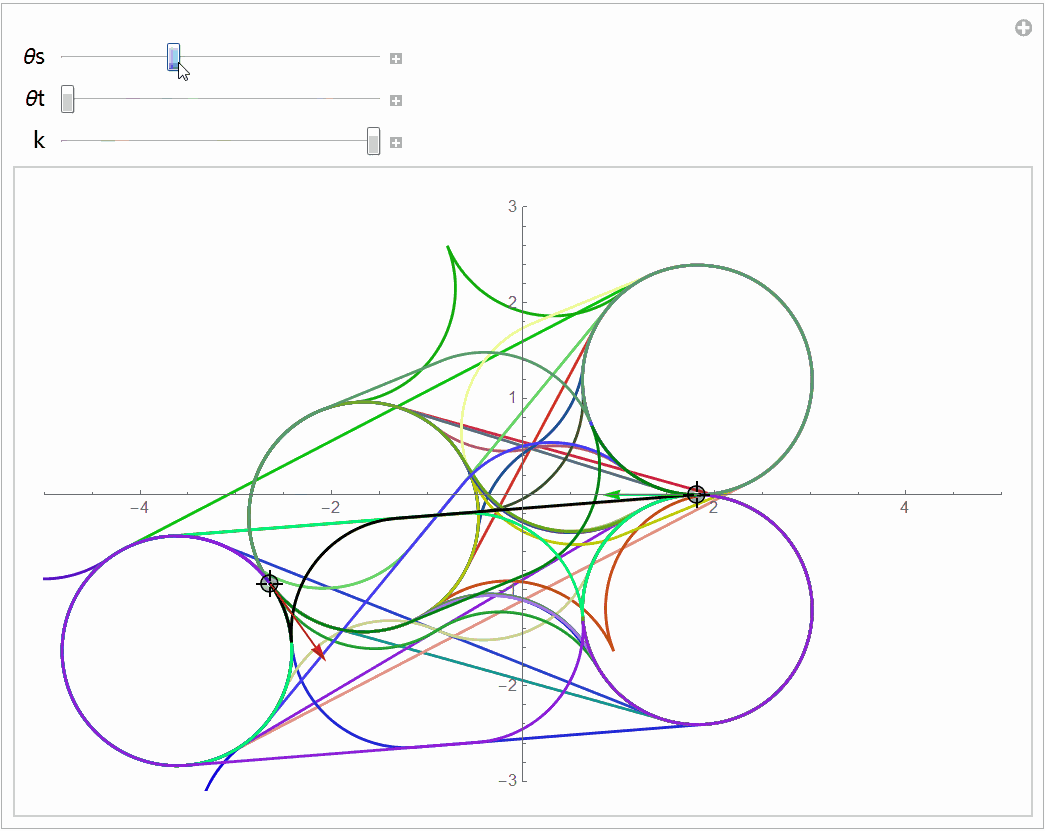
Dubins曲线是从6个曲线中选出最短的那条,而Reeds-Shepp曲线是从46个曲线中选出最短的那个,这46个曲线如下图所示。(最开始的论文认为最短的曲线一定在48条曲线中,后人研究发现有两条曲线不会是最短的,所以搜索范围减小到46条)
1.4 Mathematica代码
源代码在https://github.com/robinvista/Mathematica。你可以对起点进行扰动,观察最短曲线的不连续变化。
2 Dubins曲线
2.1 什么是Dubins曲线?
Dubins曲线和Reeds-Shepp曲线差不多,只不过多了一个约束条件:汽车只能朝前开,不能后退(不能挂倒挡)。Dubins曲线由Dubins在1957年的论文《On curves of minimal length with a constraint on average curvature and with prescribed initial and terminal positions and tangents》[2]中提出。Dubins曲线如下图所示。1957年的时候动态规划方法才刚出生,Dubins几乎是赤手空拳算出了Dubins曲线。

2.2 Dubins曲线是什么样的曲线?
Dubins曲线同样由几段半径固定的圆弧和一段直线段拼接组成,而且圆弧的半径就是汽车的最小转向半径。
3 Reeds-Shepp曲线和Dubins曲线对任意的起止位姿都存在吗?
答案是肯定的,任意的起始状态和终止状态之间都存在这样的曲线,如下图所示。这时为了清晰起见,我用箭头表示汽车的朝向,蓝色箭头是出发位姿,绿色箭头是目标位姿,黑色曲线是Reeds-Shepp曲线,红色曲线是Dubins曲线。注意二者有时是重合的。

4 当环境中存在障碍物时,Reeds-Shepp曲线和Dubins曲线对任意的起止位姿都存在吗?
Reeds-Shepp曲线和Dubins曲线特指没有障碍物时的最短路径。如果存在障碍物,那么这样的曲线不再是传统意义上的RS和Dubins曲线了,不过为了保持一致我们还是这么称呼它们吧。
生活从来没那么简单,你在停车时周围可能会有各种障碍物,比如其它车辆、垃圾桶。这时是否仍然存在RS曲线和Dubins曲线似乎没那么容易回答了。不过庆幸的是这个问题已经被人解决了,答案是:只要存在连接起止位姿的无碰撞路径,那么就存在无碰撞的Reeds-Shepp曲线。然而这个结果对Dubins曲线却不适用。这个答案好像没什么出人意料,不过稍微品味一下却让人很吃惊。注意这里的前提:“连接起止位姿的无碰撞路径”,除了无碰撞的要求以外,我没说其它任何的要求,比如存在一条类似“Z”这样完全由直线组成的折线路径也可以。很奇妙吧?不管你的路径由什么线(直线或者任意曲线)组成,不管它有多怪异多扭曲,只要你能找到一条这样的路径,那么就一定存在满足要求的Reeds-Shepp曲线,即连接起止位姿,并且汽车不会碰到障碍物。在电影《车手》中就出现了神奇的一幕——汽车原地直角拐弯。其实理论上,不需要原地拐弯,汽车也能通过狭窄的直角胡同。
理论上存在没有给我们提供实际寻找的方法,这时我们可以采用随机搜索的方法,见下图(黑色多边形表示障碍物)。
5 值函数
既然任意的起点和终点之间都存在最短曲线,现在我们考虑这样一种玩法。假如我们把终点(的位姿)固定在原点,也就是令$(x_T,y_T,{\theta}_T)=(0,0,0)$,然后改变起点(的位姿),那么这样起点与终点之间RS或者Dubins曲线的长度可以看成是起点位姿的函数,因为曲线长度只依赖起点位姿(假如转向半径是固定不变的),而且唯一依赖,所以这是符合函数的定义的,除了稍微有点奇怪大家应该没有什么太大的疑虑吧。
我们对任意起点计算这个函数的值,这样的函数是以位姿$(x,y,\theta)$为自变量的函数,它的函数值则是曲线的长度,我们就叫它值函数(Value function)吧。回过头想象最简单的情况,如果机器人或者汽车的运动不受转向半径的约束,前后左右想怎么运动就怎么运动,也就不考虑姿态角度的影响,那这样对应的值函数就是起点到终点的距离,即$\sqrt{x^2+y^2}$。这样一个二元值函数,它的图像可以在三维坐标系里画出来,没错,就是个圆锥。对于Dubins曲线和RS曲线,它们的值函数图像如下图所示。因为Dubins曲线和RS曲线的值函数依赖三个变量(也就是位姿$(x,y,\theta)$),所以它们是三元函数,没办法在三维坐标系里展示,要在四维空间才能画出来。所以没办法,这里只能画出它们在三维空间的水平集给大家感受感受。一个函数$f(x)$的水平集的定义很简单,就是满足$f(x)=c$的$x$的集合。这里$c$是个常数,对于不同的$c$,对应的水平集也不一样,我们可以把对应不同$c$的那些自变量$(x,y,\theta)$都挑出来,这样就能在三维空间里画出来了。所以下图里的图像是所有等于某个常数的位姿$(x,y,\theta)$形成的曲面,常数值也显示在图中了。
如果你听说过强化学习,这里的值函数就是强化学习中出现的值函数,即最优的累积回报。值函数有什么用呢?假如我们知道值函数,那么一直沿着值函数的梯度下降的方向运动,那最终就能到达终点,这样形成的曲线又是什么样的呢?不是别的,就是Dubins曲线和Reeds-Shepp曲线。值函数的另一个用处是作为启发函数,路径搜索算法需要这样的启发函数加快搜索速度,比如混合A* 和RRT* 等。


6 从Reeds-Shepp和Dubins曲线出发
了解了Reeds-Shepp和Dubins曲线,我们的眼光可以放远一点。其实,Reeds-Shepp和Dubins曲线只不过是最优曲线的两个特殊情况,我们可以考虑各种各样的机器人约束或者目标函数,这时的曲线就更有意思了,当然也更难了。Reeds-Shepp和Dubins曲线之所以有名,是因为它们刚好存在解析形式,而且形式还不是太复杂,类似的曲线还有Balkcom-Mason曲线。其它更复杂的最优曲线要想求解析解是非常困难的。
参考资料
[1] Optimal Paths for a Car That Goes both Forwards and Backwards,J. A. Reeds and L. A. Shepp,Pacific Journal of Mathematics.
[2] On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents,Lester E. Dubins,American Journal of Mathematics.
